焕杰的博客

噪声

2021/09/28

之前写博客喜欢排版, 浪费很多时间, 而且会导致热情消退之后懒得花时间写博客. 恰逢生活比较忙, 一段时间没写点什么了.

最近整理了博客页面, 用GLSL es3.0加了这个页面, 打算拿着色器写噪声, 用来展示效果, 很方便. 写的编辑框好像有bug, 建议还是编辑器写, 网页验证结果. 此外这玩意儿在手机上行不通, 能画, 但是结果不对, 不知道是不是精度问题.

1. 随机数, 白噪声

这篇文章我计划一点点更新, 把常见的几个噪声加进去. GLSL里需要手搓随机数, 常用的有这么几个hash方法.

1
2
3
4
5
6
float hash11(float n){ return fract(sin(n) * 43758.5453123); }
float hash12(vec2 p) { return fract(sin(dot(p, vec2(12.9898, 78.233))) * 43758.5453); }
vec3 hash33(vec3 p) {
    p = mat3(127.1, 269.5, 113.5, 311.7, 183.3, 271.9, 74.7, 246.1, 124.6) * p;
    return fract(sin(p) * 43758.5453123) * 2. - 1.;
}

虽然静止的噪声看上去没啥问题, 但是当我在参数中掺上时间, 再画出来不难发现, 这两个函数都有比较明显的瑕疵, 肉眼看上去感觉图片总在往一个方向移动. 我找到了另一个使用位操作的噪声, 来源网址.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
uint hash(uint x) {
    x += (x << 10u);
    x ^= (x >> 6u);
    x += (x << 3u);
    x ^= (x >> 11u);
    x += (x << 15u);
    return x;
}
float uintToFloat(uint x) {
    const uint mantissaMask = 0x007FFFFFu;
    const uint floatOne = 0x3F800000u;
    x &= mantissaMask;
    x |= floatOne;
    return uintBitsToFloat(x) - 1.0f;
}
uint hash(uvec2 v) { return hash(v.x ^ hash(v.y)); }
uint hash(uvec3 v) { return hash(v.x ^ hash(v.y) ^ hash(v.z)); }
uint hash(uvec4 v) { return hash(v.x ^ hash(v.y) ^ hash(v.z) ^ hash(v.w)); }
float random(float x) { return uintToFloat(hash(floatBitsToUint(x))); }
float random(vec2 v) { return uintToFloat(hash(floatBitsToUint(v))); }
float random(vec3 v) { return uintToFloat(hash(floatBitsToUint(v))); }
float random(vec4 v) { return uintToFloat(hash(floatBitsToUint(v))); }

最终结果. 原文提到这个噪声均值在0.5附近, 而且无论我怎么变换time值, 结果上都没看到明显的特征. 感觉不错, 但到白噪声才刚刚开始, 就用这个随机数继续写其他噪声好了.

2. Perlin噪声

原始的Perlin噪声为了满足伪随机多次调用给出相同结果的特性, 用了一个shuffle数组. 在GLSL里写这玩意儿不方便, 而且会限制住坐标的范围, 我就直接用上一步写的hash了.

在空间中定义一个间距均等的网格, 为每个格点分配一个随机向量作为它的“梯度”, 对于方格内的点, 分别计算四个角点到该点的向量点乘其随机向量的积, 把四个角点上的噪声值按照点积的结果进行平滑插值, 得到每个点上的噪声值.

假设对于点 $ p(x,y) $ 有: \[ x_0 = \lfloor x \rfloor, x_1 = \lceil x \rceil, \\ y_0 = \lfloor y \rfloor, y_1 = \lceil y \rceil ; \] 则与其相邻的四个角点可定义为: \[ p_{00}(x_0, y_0), p_{01}(x_0, y_1), p_{10}(x_1, y_0), p_{11}(x_1, y_1) \] 设四个角点的随机向量为 \(d_{00}, d_{01}, d_{10}, d_{11}\) . 则这四个角点对于目标点的噪声值的贡献度分别为: \[ \begin{align} c_{00} & = \overrightarrow{p_{00}p} \cdot \vec{d_{00}} \\ c_{01} & = \overrightarrow{p_{01}p} \cdot \vec{d_{01}} \\ c_{10} & = \overrightarrow{p_{10}p} \cdot \vec{d_{10}} \\ c_{11} & = \overrightarrow{p_{11}p} \cdot \vec{d_{11}} \end{align} \]

对于平滑插值的函数, Perlin最早使用的是 \(3t^2 + 2t^3\), 即smoothstep方法的曲线, 但是其导数有线性分量导致结果不够自然, 后来建议使用更加平滑的 \(6t^5 - 15t^4 + 10t^3\) 进行插值. \[ fade(t) = 6t^5 - 15t^4 + 10t^3 = ((6t - 15) t + 10) t^3 \] 则点 \(p\) 的噪声值 \(r\) 为: \[ \begin{align} r_{x0} = & fade(c_{00}, c_{10}, x) \\ r_{x1} = & fade(c_{10}, c_{11}, x) \\ r = & fade(r_{x0}, r_{x1}, y) \end{align} \]

上面举的例子是二维的, 但这个方法不限制维数, 只是插值次数会随维数增大形成指数增长. 这里贴一个三维实现, 第三维用的时间.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#define OCTAVES 4
precision highp float;
precision highp int;
uniform float time;
uniform vec2 resolution;
out vec4 fragColor;
uint hash(uint x) { x += (x << 10); x ^= (x >> 6); x += (x << 3); x ^= (x >> 11); x += (x << 15); return x; }
uint hash(uvec3 v) { return hash(v.x ^ hash(v.y ^ hash(v.z))); }
float parseFloat(uint x) { return uintBitsToFloat((x & 0x007FFFFFu) | 0x3F800000u) - 1.0f; }
float random(float x) { return parseFloat(hash(floatBitsToUint(x))); }
float random(vec3 v) { return parseFloat(hash(floatBitsToUint(v))); }
float fade(float t) { return ((6.0f * t - 15.0f) * t + 10.0f) * t * t * t; }
vec3 getVec(vec3 pos) {
    pos = mat3(127.1f, 269.5f, 113.5f, 311.7f, 183.3f, 271.9f, 74.7f, 246.1f, 124.6f) * pos;
    return normalize(vec3(random(pos.xyz), random(pos.yzx), random(pos.zxy)) * 2.0f - 1.0f);
}
float perlin(vec3 pos) {
    vec3 p0 = floor(pos), d = fract(pos), e = vec3(1.0f, 0.0f, 0.0f);
    float fx = fade(d.x), fy = fade(d.y), fz = fade(d.z);
    float g0 = dot(d - e.yyy, getVec(p0 + e.yyy)), g1 = dot(d - e.xyy, getVec(p0 + e.xyy)),
          g2 = dot(d - e.yxy, getVec(p0 + e.yxy)), g3 = dot(d - e.xxy, getVec(p0 + e.xxy)),
          g4 = dot(d - e.yyx, getVec(p0 + e.yyx)), g5 = dot(d - e.xyx, getVec(p0 + e.xyx)),
          g6 = dot(d - e.yxx, getVec(p0 + e.yxx)), g7 = dot(d - e.xxx, getVec(p0 + e.xxx));
    float result = mix(mix(mix(g0, g1, fx), mix(g2, g3, fx), fy),
                       mix(mix(g4, g5, fx), mix(g6, g7, fx), fy), fz);
    return result + 0.5f;
}
void main() {
    vec3 pos = vec3(gl_FragCoord.xy / resolution.y, time * 0.2f) * 3.0f;
    float noise = 0.0f, multiply = 1.0f, scale = 0.0f;
    for (int i = 0; i < OCTAVES; i++) {
        scale += multiply;
        noise += multiply * perlin(pos);
        pos *= 2.0f;
        multiply *= 0.5f;
    }
    fragColor = vec4(vec3(noise / scale), 1.0f);
}

效果预览在这里. 关于噪声函数结果值的归一化, 在一维情况下考虑输入在 \([0, 1]\) 上的极端情况可以发现, 结果的噪声值在范围 \([-\frac{1}{2}, \frac{1}{2}]\) 之间, 因此直接 +0.5f 使结果落在范围 \([0, 1]\) 上. 这里顺便加了分形, 每次叠加一个频率翻倍强度减半的噪声, 以达到添加细节模拟自相似的效果.

3. Simplex噪声

Simplex噪声是Perlin噪声的改进版, Perlin噪声在高维下需要插值的点数呈指数增长, 因此在Simplex噪声中不再使用正交网格的格点, 而是使用单形的顶点插值, 这样需要计算的点数只有维数+1个. 此外Simplex中使用一个径向衰减函数替代了原本的插值, 只需要对所有点求和即可.

问题在于如何确定空间中一个点到它所属单形的所有顶点的距离怎么算, 也就是需要求出单形顶点的坐标. 可以通过拉伸正交网格, 并判断各个分量的大小关系算出, 这里无耻地偷图, 举一个二维的例子.

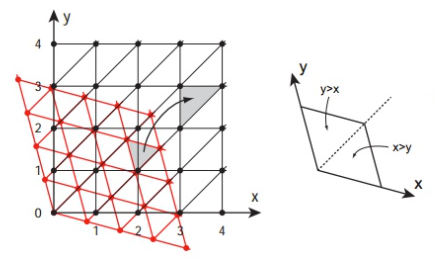
拉伸正方形得到二维坐标系下的单体

正方形网格只是用来定义单形网格的, 噪声采样的点实际位于单形网格中. 想求出所在三角形的三个顶点坐标, 可以先将点P拉伸至正方形网格, 求得所在的直角三角形三个顶点坐标, 再还原至单形网格下的坐标即可.

回到一般情况, 设n为维数, 通过偏斜可以得到单形网格和正交坐标系网格之间的关系, 对于单形网格内的点P可以通过 \[ P' = P + (P_x + P_y + ...) \times \frac{\sqrt{n + 1} - 1}{n} \] 来计算对应在正交网格下的点P'的坐标; 反过来已知P'在正交网格下的坐标, 可以通过 \[ P = P' - (P'_x + P'_y + ...) \times \frac{1 - 1/ \sqrt{n + 1}}{n} \] 来计算出位于单形网格内的P点的坐标.

找点的问题解决了, 就可以求噪声值了, 设\(\overrightarrow{dist}\)为目标点到当前单形顶点的距离向量, \(\overrightarrow{grad}\)为当前单形顶点的随机梯度向量, 求和过程可以表示为: \[ N = \sum{(max(0, r^2 - |\overrightarrow{dist}|^2))^4 \times dot(\overrightarrow{dist}, \overrightarrow{grad})} \] 其中\(r^2 - |\overrightarrow{dist}|^2\)这部分被称为径向衰减, 有趣的是不论维度为多少, 点到对边或对面的距离一直是\(\frac{\sqrt{2}}{2}\), 因此\(r^2\)取值为0.5可以确保没有不连续的间断点, 但是取值为0.6效果更好; 后面的点积和Perlin噪声中的思路一致.

归一化, 需要知道噪声的取值范围, 我数学不好, 参考了catlikecoding里的做法, 可疑的点有边中点, 面重心和正四面体的重心, 分别在\(r^2\)取值0.5和0.6的情况下计算噪声最值, 发现边中点的取值范围更大, 最大值约为0.025077, 因此对结果放大40倍即可.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#define OCTAVES 1
precision highp float;
precision highp int;
uniform float time;
uniform vec2 resolution;
out vec4 fragColor;
uint hash(uint x) { x += (x << 10); x ^= (x >> 6); x += (x << 3); x ^= (x >> 11); x += (x << 15); return x; }
uint hash(uvec3 v) { return hash(v.x ^ hash(v.y ^ hash(v.z))); }
float parseFloat(uint x) { return uintBitsToFloat((x & 0x007FFFFFu) | 0x3F800000u) - 1.0; }
float random(float x) { return parseFloat(hash(floatBitsToUint(x))); }
float random(vec3 v) { return parseFloat(hash(floatBitsToUint(v))); }
float fade(float t) { return ((6.0 * t - 15.0) * t + 10.0) * t * t * t; }
vec3 hash33(vec3 pos) {
    pos = mat3(127.1, 269.5, 113.5, 311.7, 183.3, 271.9, 74.7, 246.1, 124.6) * pos;
    return normalize(vec3(random(pos.xyz), random(pos.yzx), random(pos.zxy)) * 2.0 - 1.0);
}
float simplex(vec3 pos) {
    const float K1 = 0.3333333;
    const float K2 = 0.1666667;
    vec3 p = floor(pos + dot(pos, vec3(K1)));
    vec3 x0 = pos - (p - dot(p, vec3(K2)));
    // nice solution from https://www.shadertoy.com/view/XsX3zB
    vec3 e = step(0.0, x0 - x0.yzx);
    vec3 i1 = e * (1.0 - e.zxy);
    vec3 i2 = 1.0 - e.zxy * (1.0 - e);
    vec3 x1 = x0 - (i1 - K2);
    vec3 x2 = x0 - (i2 - 2.0 * K2);
    vec3 x3 = x0 - (1.0 - 3.0 * K2);
    vec4 h = max(0.6 - vec4(dot(x0, x0), dot(x1, x1), dot(x2, x2), dot(x3, x3)), 0.0);
    vec4 r = vec4(dot(x0, hash33(p)), dot(x1, hash33(p + i1)), dot(x2, hash33(p + i2)), dot(x3, hash33(p + 1.0)));
    return 0.5 + dot(h * h * h * h, r) * 20.0;
}
void main() {
    vec3 pos = vec3(gl_FragCoord.xy / resolution.y, time * 0.2) * 3.0;
    float noise = 0.0, multiply = 1.0, scale = 0.0;
    for (int i = 0; i < OCTAVES; i++) {
        scale += multiply;
        noise += multiply * simplex(pos);
        pos *= 2.0;
        multiply *= 0.5;
    }
    fragColor = vec4(vec3(noise / scale), 1.0);
}

最终结果

这里额外解释下i1和i2这两个变量, 主要是怕自己忘, 一个正方体可以拉伸为6个正四面体, 逐一判断大小很麻烦, 而且shader里if语句代价不小.

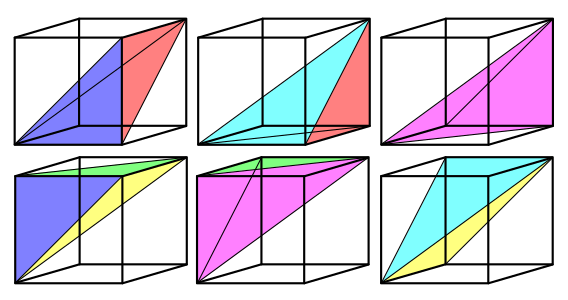
一个正方体可以拉伸为6个正四面体

这两个向量分别可以看作(x>z&&x>y, y>z&&y>x, z>x&&z>y), (x>z||x>y, y>z||y>x, z>x||z>y), 空间上可以理解为x0的最大分量决定距离(0,0,0)较近的顶点, 最大和次大的两个分量决定距离(0,0,0)较远的顶点, 结合(0,0,0)和(1,1,1)形成四面体, 很巧妙的方法.

参考 & 感谢

Random Floats in GLSL 330

GLSL - 噪声算法的收集

flow by Perlin noise - Shadertoy

Simplex Noise, keeping it simple

Perlin噪声与Simplex噪声笔记

Simplex Noise（一）

3d simplex noise - Shadertoy

Total : 7
2021
2020
cocos shader algorithm